What is Riemann Sum?

Riemann Sums is a special type of approximation of the area under a curve by dividing it into multiple simple shapes like rectangles or trapezoids and is used in integrals when finite sums are involved. Figuring out the area of a curve is complex hence this method makes it simple. Usually, we take the help of different integration methods for this purpose. This is one of the major parts of integral calculus. 

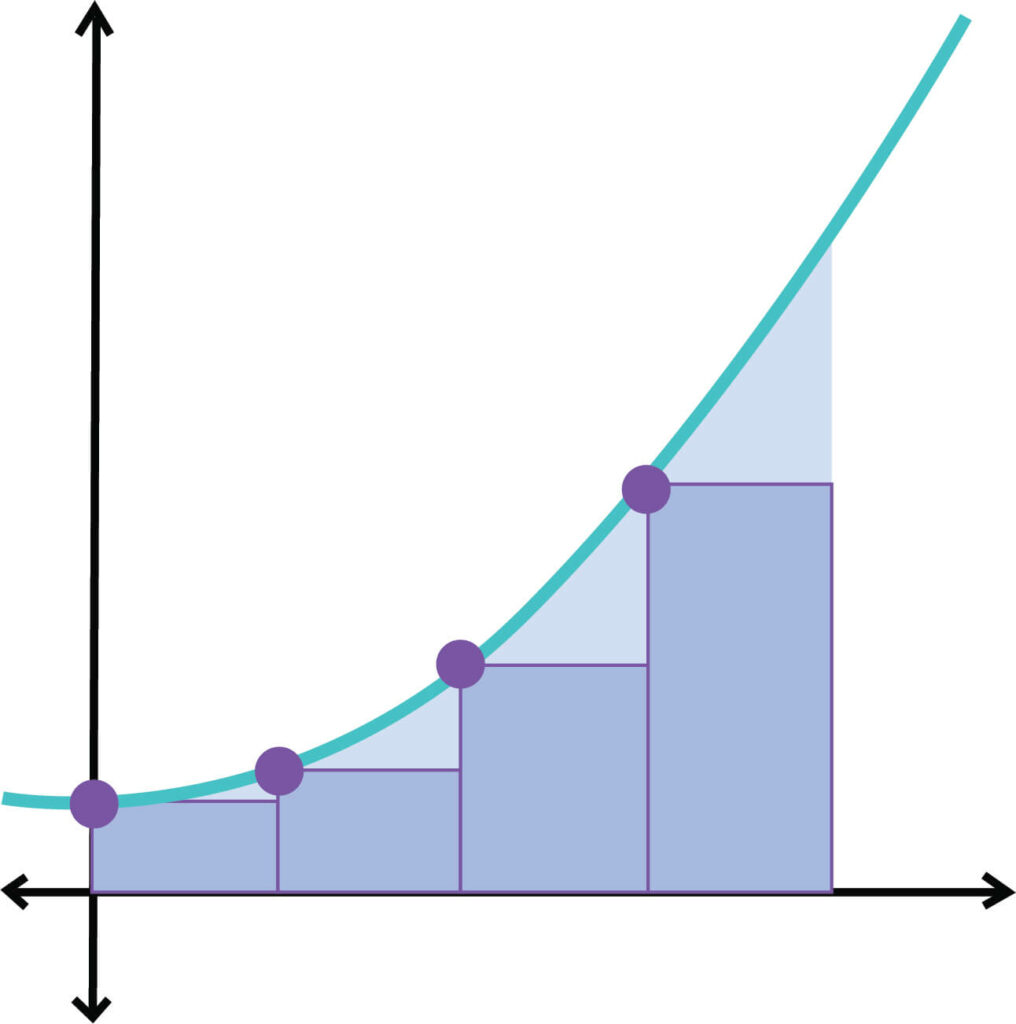
In the nineteenth century, well-known German mathematician Bernhard Riemann came up with this brilliant method of finding out the area under the curve. As a result, this approximation process was named after him. At present, it is a major part of the calculus syllabus. 

How many types of Riemann Sums are there? 

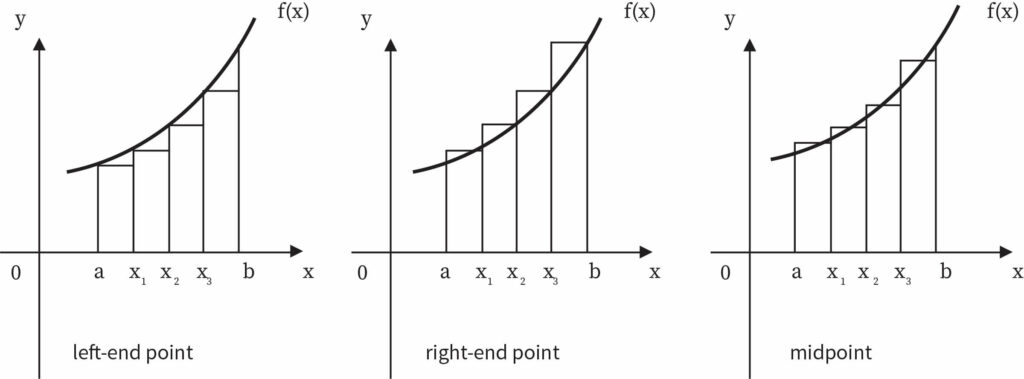
There are mainly three categories in which the Riemann Sums can be classified. They are the left, right, and midpoint Riemann sum.

Left Riemann Sum 

To create a Riemann sum, selecting the way to form rectangle is necessary. The curve which touches the top-left corner to form the rectangle is known Left Riemann sum.

Right Riemann Sum 

The way to form rectangle is to touch the curve with their top-right corners. This is called a Right Riemann sum.

Midpoint Riemann Sum 

Similarly, in a midpoint Riemann Sum, the functional value at the base midpoint is considered. Each chosen rectangle has heights equal to this value. The height of each rectangle is equal to the value of function at the midpoint of its base.

What are the other Methods of finding Riemann Sum?

Alternatively, there is also the option for using other shapes than rectangles. Mainly trapezoids are used for this purpose. The rule of approximating the area of the curve using trapezoids is also known as the trapezoidal rule. In such cases, each of the trapezoids must be placed in such a manner that both the top vertices of the trapezoid are in contact with the curve. 

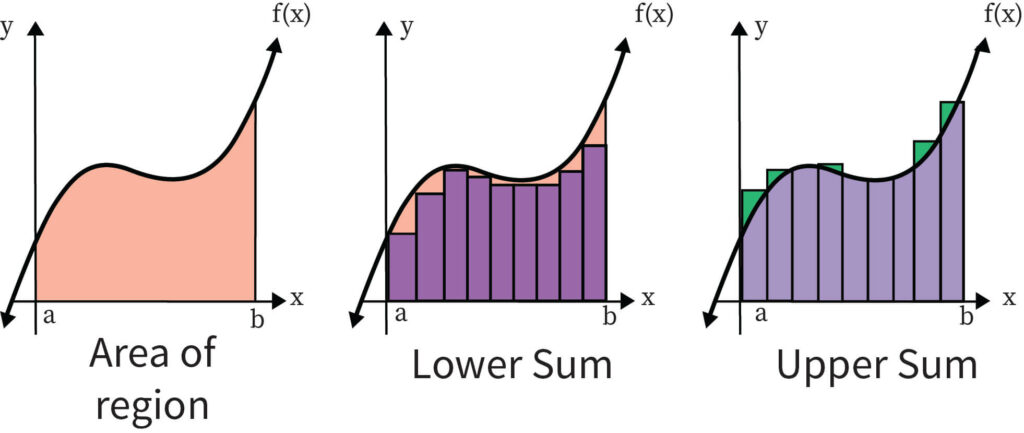
In general, any kind of approximation can be done to find out the Riemann Sum. In practice, it has been seen that with the use of more shapes, the approximation of the real area has improved. While finding out the area under the curve, resources will differ. However, a Riemann Sum is generally found out by using the rectangular shape. Alternatively, it is known as a trapezoidal sum when trapezoids are used to approximate the area. 

Formulas

Summation Notation 

In general, the summation notation can be expressed as

$k={\displaystyle \sum _i^{j}f\left(k\right)}=f\left(i\right)+f\left(i+1\right)+f\left(i+2\right)+\mathrm{...}+f\left(j\right)$

This term is used to represent the addition of each of the terms of the summand, which is $f_k$. This summation process takes place when the value of k is increased. This increase in value starts from the lower bound and ends in the upper bound, which are i and j respectively. Basically, the summation takes place between these two limits. The summand $f_k$ denotes that its value is dependent on the value of the k index.

Monotonically decreasing function

Similarly, in some cases, with the increase in the value of the independent variable, the dependent variable may not increase. In this case, the function is known as a monotonically decreasing function.

Partition

This is an important concept that we use in finding out Riemann Sums. In this case, a partition is created that divides the given interval into multiple new intervals. This is usually done when the approximation process in the newly found intervals can be done in an easier manner. The area under all these intervals is found out simultaneously. After that, the summation of the area under all these intervals will give the area of the defined interval.

For example, if there is an interval$\left[t_1,t_5\right]$, and we have a partition$P=\left\{t_1,t_2,t_3,t_4,t_5\right\}$, then the initial interval can be portioned into 4 new intervals. These new intervals will be$\left[t_1,t_2\right]$, $\left[t_2,t_3\right]$ , $\left[t_3,t_4\right]$ and $\left[t_4,t_5\right]$ respectively.

Riemann Sum Notation 

In general, it is denoted by:

$S={\displaystyle \sum _{k=1}^{n}f\left(k\right)}=f\left(x\times k\right)\left(x_k-x_{k-1}\right)$

In this notation, the domain has been divided into a total of ‘n’ sub-intervals. Each interval has been so chosen that the area of the rectangle can be calculated. The rectangle is extended from the x-axis up to a height of the functional value of $f\left(x\times k\right)$. Similarly, the width of the rectangle is equal to the width of the $\left(x_k-x_{k-1}\right)$sub-interval.

This explains that any value of x can be chosen within the chosen sub-intervals. Also, there is the option of keeping different lengths of different sub-intervals. However, it is much easier to find out the Riemann sums for whom the sample points are standardized and the lengths of the sub-intervals are chosen.

Practice Problem

For an integer i such that i is greater than 1, let the numbers $\left\{x_i\right\}$ be defined as $x_i=2i-1$.

Evaluate ${\displaystyle \sum x_i}$, for $i=1,2,3,4$.

We solve the problem by putting the value of i as 1, 2, 3, and 4. Then we find out the sum.

Hence,

$\begin{array}{c}{\displaystyle \sum x_i}=x_1+x_2+x_3+x_4\\ =1+3+5+7\\ =16\end{array}$

This is the required answer.

Context and Applications

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for

• B.Sc Mathematics
• M.Sc Mathematics