What is meant by mass transfer?

The concept of mass transfer is generally used in engineering disciplines especially in chemical engineering that involves the transport of chemical species through the phenomena of convection and diffusion. Chemical species are those substances that are composed of identical molecular entities. Mass transfer is the movement of mass from one point of a specific location in space to another, and it may take place both in single-phase systems and multiphase systems. Transfer of mass usually means the movement of streams, phases, and a fraction of molecules of a component to another, especially due to concentration gradient. Evaporation, precipitation, absorption, drying, membrane filtration, diffusion, convection, and distillation are some of the processes where mass transfer takes place.

In most of the practical problems encountered in chemical engineering, mass transfer generally occurs along with chemical reactions, and the flux of a chemical species does not remain conserved as the chemical species in a chemical reaction never remains constant. The mass transfer theory allows engineers to compute the mass flux in a system and its distribution over the entire system; this accounts for better designing and control of chemical systems.

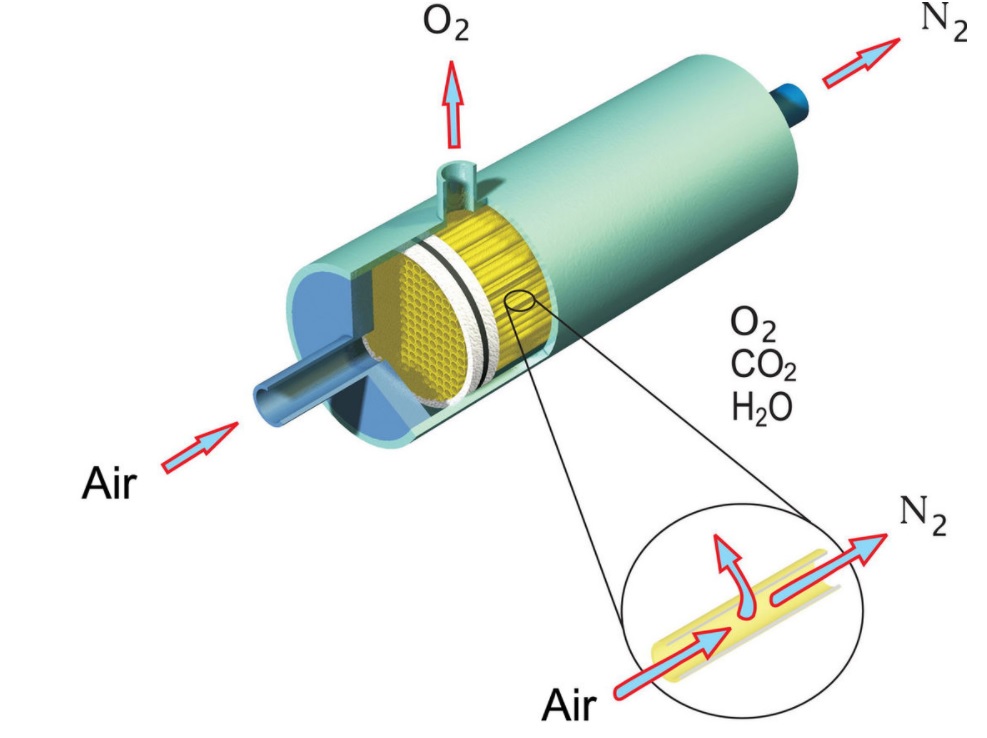
Analysis

The mass transfer also finds its specialized analysis in the area of reaction engineering, separation engineering, electrochemical engineering, and heat and mass transfer engineering. The fundamental driving entity of mass transfer in the presence of concentration gradient or difference in concentration of the species involved. In a single-phase system, the molecules move by the phenomena of diffusion from a high concentration gradient to a lower concentration gradient till the composition gets uniform. In a multiphase system, the mechanism follows the same as that of a single-phase system, but the diffusion continues to occur till all the species involved are absorbed in one of the phases making the concentration uniform.

The transport phenomena

The transport phenomena are concerned with the exchange of mass, energy (heat), and momentum between various systems. The fundamental principle governing the analysis of such systems follows that the parameters remain conserved before and after the process. There are some similarities involved in the analysis of heat, mass, and momentum transfer. Newton's momentum transfer equations, Fick's law governing the mass transfer, and Fourier law governing heat transfer are approximately similar. These laws consider linear approximations of the conserved quantiles in a certain flow field.  At higher Reynold's number, the Naiver-Stokes's equation approaches non-linearity. Hence, the analogy between heat, mass, and momentum transfer becomes less similar, but the similarity between heat and mass transfer remains unaltered. Reynolds number is an important parameter that decides whether the given flow regime is laminar or turbulent. It is the ratio between inertia force and viscous force. The term inertia forces indicate the forces generated when particles of fluid at a certain velocity collide with each other, hence their state of inertia changes. High turbulence indicates high particle velocity and hence, higher inertia forces. A high viscous force indicates high viscosity of the fluid, i.e., the fluid possesses greater cohesive forces. A stationary fluid mass in a media may possess viscosity but the inertia forces are zero. 

Modes of mass transfer

The two fundamental modes of mass transfer are:

• Diffusion
• Convection

Diffusion

Diffusion is a phenomenon that makes the concentration profile of a medium involving chemical species distribute uniformly over time. A concentration profile governs the density of a certain chemical species in a particular space at a certain time interval. The species involved in the process usually remains in the form of a solution, with each of the species behaving like a solute. Thermal agitation is the driving potential for diffusion phenomena, and it is the primary contributor to mass transfer rates. Molecules in a system above the absolute zero temperature never remain at rest, they are always accompanied by molecular motion possessing a certain velocity. This motion of molecules leads to randomized collisions and velocity alterations. The presence of a driving force like concentration pushes these molecules towards a low concentration area increasing the flow rate, as a consequence of this increased flow rate, molecules collide with other molecules in that area transferring a part of their energy, which leads to diffusion. This rate of motion is directly a function of temperature and concentration.

Convection

Mass transfer by convection is the transport of mass between a flowing fluid and the boundary surface of either a solid or a liquid. Mass transfer through convection also occurs between two fluids in motion, which have poor solubility. There are generally two characteristics of mass transfer, they are:

• Convective mass transfer occurs in a single phase to form a phase boundary.
• Convective mass transfer is similar to diffusion with combined effects of advection. Where, advection refers to the transport of quantity due to bulk fluid motion, or macroscopic movement of fluid particles.

Fick's law of diffusion

Fick's law of diffusion is the fundamental law that governs the mass transfer phenomena through diffusion. According to the law, The diffusion flux of particles in a mixture from a high concentration to a lower concentration depends directly on the concentration gradient. 

Mathematically the Fick's law is expressed as,

${\lambda }_D=-\psi \frac{d\theta }{dx}$

where

${\lambda }_D$ denotes the diffusion flux. Here, the subscript $D$ refers to diffusion phenomena.

The constant of proportionality is removed by introducing a constant.

Therefore, the equation can be written as $\lambda =-\psi \frac{d\theta }{dx}$

where the constant $\psi$ denotes diffusion coefficient or diffusivity, $d\theta$ denotes the change in concentration of the particles and $dx$ denotes the change in position of particles due to diffusion phenomena.

The negative sign before the diffusivity represents the movement of particles from a higher concentration side to a lower concentration side. The diffusivity decides the mass transfer rates. 

Diffusion in porous media

A porous media is a medium associated with voids or spaces between its molecules. Phenomena such as the gas-phase diffusion in porous media are significant in the multiphase flow of fluids, which allows transport of contaminants in the subsurface of the medium. The gas-phase diffusion process finds its application in two of the most important process, removal of non-aqueous phase liquid (NAPL) contaminants from low-permeability layers present in the subsurface, analysis of contaminant migration, or drying in nuclear waste repositories. 

The use of proper models proposed by various researchers allows for the efficient analysis of such phenomena, For instance, the adjective-dispersive model (ADM) is widely used. This is based on the linear calculations based on the advection given by Darcy's law and diffusion rates given by Fick's law.

Context and Applications

The topic finds its wide application in various undergraduate and postgraduate degree courses of:

• Bachelors in Technology (Chemical Engineering)
• Masters in Technology (Chemical Engineering)
• Masters in Technology (Reaction Engineering)

Practice Problems

1. Which of the following is true regarding diffusion?

1. It is a macroscopic phenomenon.
2. It occurs from higher concentration to lower concentration.
3. Fick's law governs the phenomena of diffusion.
4. All of these

Answer: Option d

Explanation: Diffusion is a macroscopic phenomenon that is governed by Fick's law. The law states that diffusion occurs from higher concentration to lower concentration in presence of a concentration gradient.

2. When a certain fluid mass is stationary what is the nature of its inertia force?

1. Low
2. High
3. Zero
4. None of these

Answer: Option a

Explanation: When a certain fluid mass is stationary, the nature of inertia force is low and not completely zero. The phase of fluid above absolute zero temperature is always accompanied by molecular motion possessing a certain velocity. Hence, there are collisions at minute levels.

3. What is the abbreviation of NAPL?

1. Non-aqueous phase liquid
2. Non-advective porous liquid
3. Non-aqueous porous liquid
4. None of these

Answer: Option a

Explanation: The correct abbreviation for NAPL is non-aqueous phase liquid.

4. What does high inertia force indicate in Reynold's number?

1. Higher velocity and higher collisions
2. Lower velocity and lower collisions
3. Higher velocity and lower collisions
4. Lower velocity and higher collisions

Answer: Option a

Explanation: A higher inertia force in Reynold's number indicates a higher velocity and higher collisions among the fluid particles.

5. What is the correct expression for Fick's law of diffusion?

1. ${\lambda }_D=\psi \frac{d\theta }{dx}$
2. ${\lambda }_D={\psi }^2\frac{d\theta }{dx}$
3. ${\lambda }_D=-\psi \frac{d\theta }{dx}$
4. ${\lambda }_D=-\frac{1}{\psi }\frac{d\theta }{dx}$

Answer: Option c

Explanation: The correct expression for Fick's law of diffusion is ${\lambda }_D=-\psi \frac{d\theta }{dx}$