What are ideal and real gases?

Ideal gases obey conditions of the general gas laws under all states of pressure and temperature. Ideal gases are also named perfect gases. The attributes of ideal gases are as follows,

• Ideal gases reside in negligible volume.
• There is no intermolecular interaction between the ideal gases.

The gases which do not obey conditions of the general gas laws yet be liable towards ideality at low pressure and high temperature are recognized as real gases or non-ideal gases.

Simple gas laws

Boyle's law

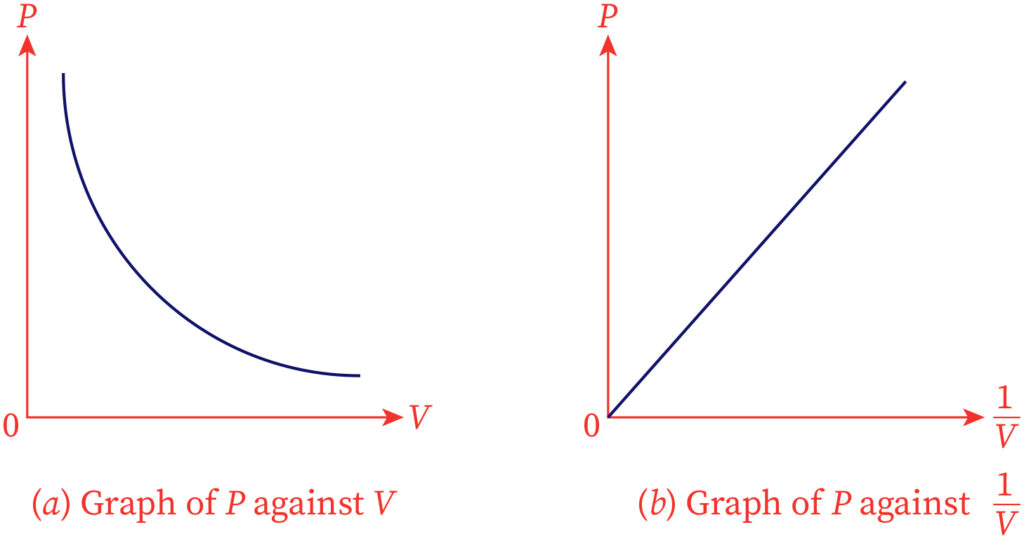
In the year 1662, Robert Boyle developed Boyle's law. Boyle’s gas law expresses that the gaseous pressure at a steady temperature is inversely relative to the volume of a gas. For a gas, the connection among pressure and molecular volume at a steady temperature is expressed numerically as,

P α 1/V

Here, the compressibility experienced by the gas is represented as P, and the volume is represented as V. By adding a constant K this proportionality can be changed.

P= k(1/V)  

PV= K

The graph of molecular volume versus pressure for a fixed measure of gas kept at a steady temperature is represented underneath,

Charle's Law

In the year 1780, Jacques Charles developed Charles's law. Charle's law expresses that at constant pressure, the gas volume is directly relative to the temperature. For a gas, the connection among temperature and capacity of the given gas (volume) at steady pressure is articulated numerically as,

V α T

Thus, this implies:

V/T= K

Here, the gaseous volume is represented as V, the temperature is represented as T and k is the compressibility factor.

Avogadro’s Law

Avogadro's law is named after Amedeo Carlo Avogadro, an Italian researcher. He recommended that two unique ideal gases possessing a similar volume at steady pressure and temperature should contain equivalent molecules.

Avogadro's Law gas law expresses that the absolute quantity of gaseous atoms is directly corresponding to gas total volume at steady pressure and temperature. For a gas, the connection among the sum of molecules and volume at steady temperature and pressure can be uttered numerically as,

V α n 

 V/n=K

Here, the volume of the applied gas is represented as V and the number of molecules is represented as n, and compressibility factor k is introduced.

The graphical portrayal of Avogadro's law is shown below.

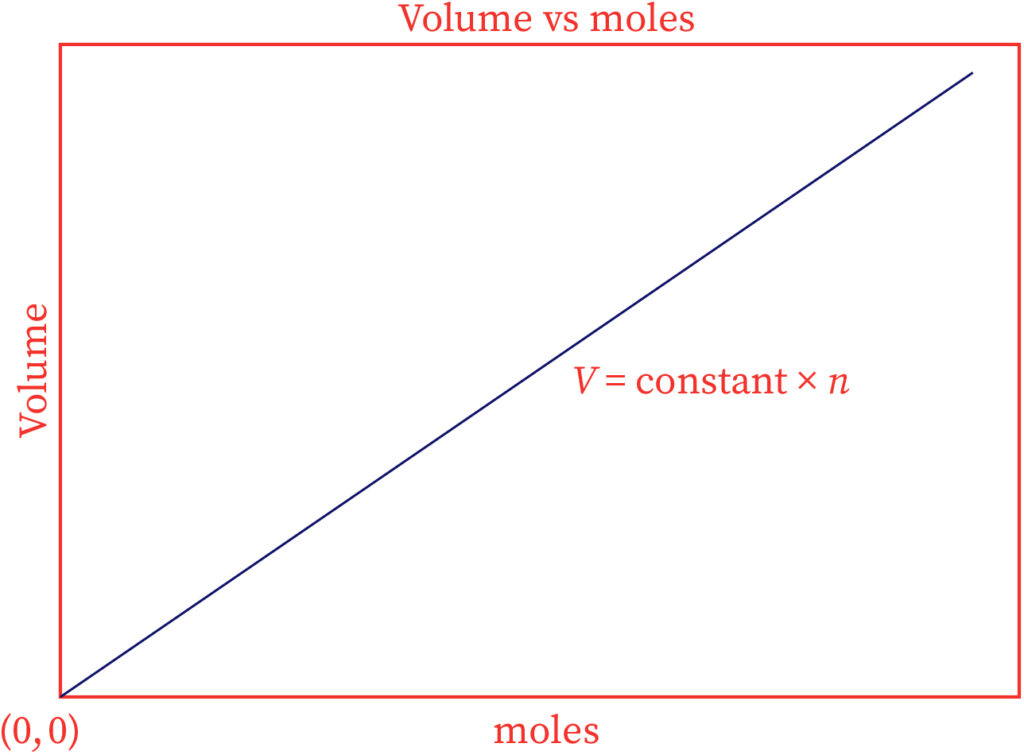
Here, the straight line goes through the beginning, suggesting that zero moles of gas will take up zero volume.

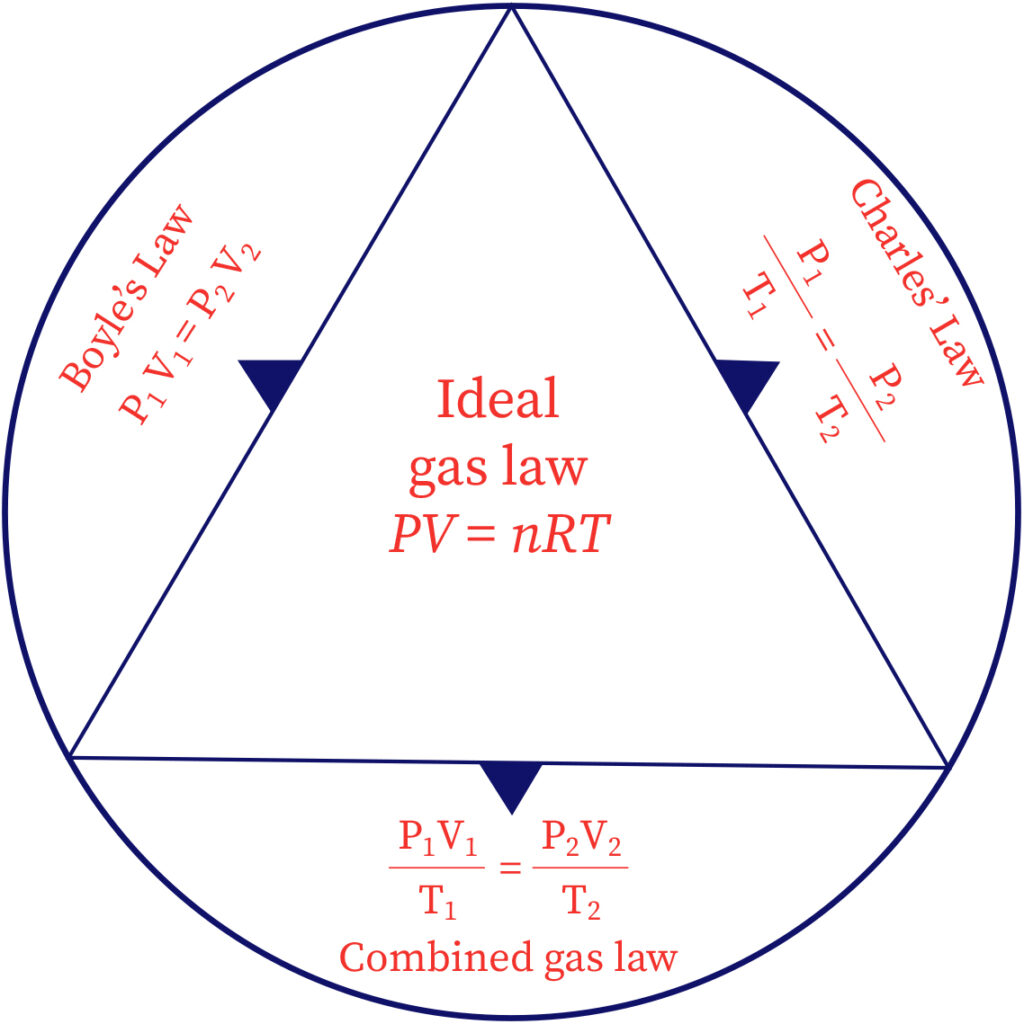
Ideal gas equation

The ideal gas law is basically a mixture of all simple gas laws such as Boyle's law, Avogadro's law, and Charles' law. The perfect gas condition can be composed as,

PV=nRT

Here, the applied gas volume is represented as V; the number of moles is represented as n; the gas temperature is represented as T and, the compressibility experienced by the gas is represented as P, universal gas constant is R.

Derivation of perfect gas equation

The ideal gas law is gotten from the work of scientists who proposed the above discussed simple gas laws. Consolidating their perception into a solitary articulation we show up at the perfect gas condition which depicts every one of the connections all the while.

The three articulations are as per the following:

According to Boyle's Law,

P α 1/V

As per Charle's Law,

V α T

According to Avogadro’s Law,

V α n

Consolidating these three articulations, we get,

V α nT/P

The above condition tells that volume is directly corresponding to the moles and the temperature while inversely relative to the pressure.

This articulation can be modified as follows:

V= R/nTP   

 V= nRT/P

Multiplying, two sides by P to clean up the portion, we get,

PV= nRT

The above condition is accepted as the ideal gas condition.

Real Gases

The condition PV= nRT is gotten from the assumptions of the kinetic hypothesis of gases and it is considerable for ideal gas only. Under low pressure and elevated temperature real gases approximately obey this condition.

Deviations of real gases from ideal behaviour

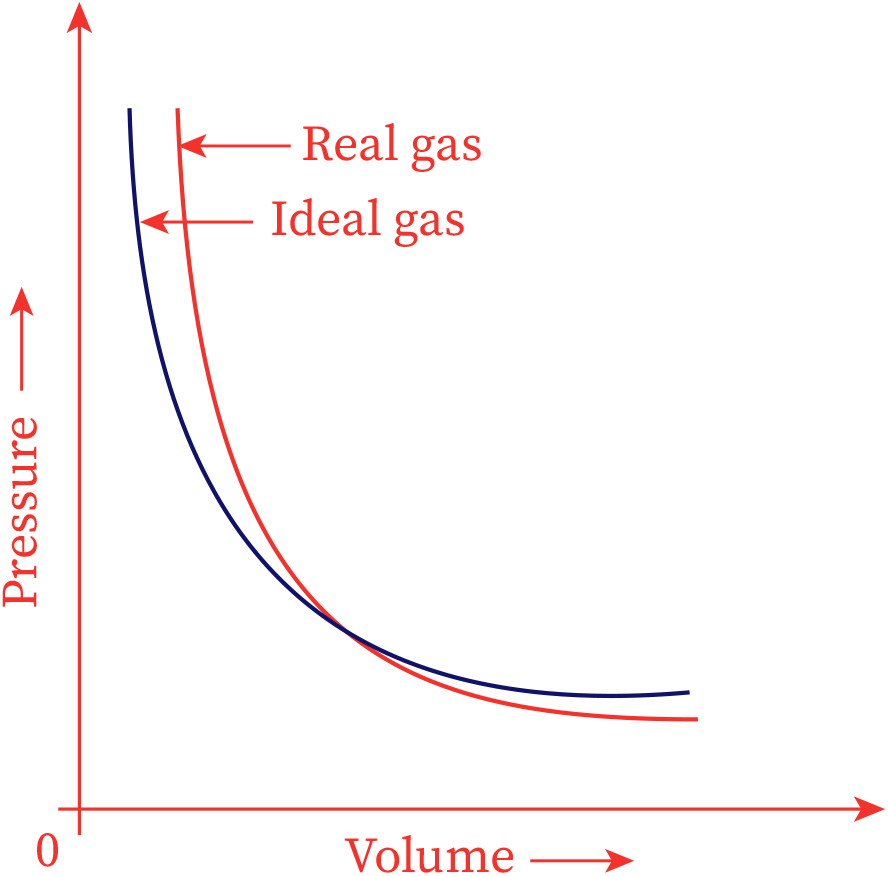
Real gases diverge from perfect gas behavior at low temperatures and high pressure. In1873, Johannes van der Waals fostered a clarification for deviations of non-ideal gases from perfect gas behavior.

Van der Waals understood that two of the presumptions of the kinetic molecular hypothesis were unclear. As per the kinetic theory, molecules involve an insignificant part of the absolute volume. It likewise accepts that the intermolecular forces between gas atoms are zero.

The volume of the non-ideal gas is excessively huge at elevated pressure. Waals corrected the volume by taking away an expression from the total volume of the non-ideal gas before substituting it into the perfect gas condition. In this manner, he presented a steady constant (b) into the perfect gas condition that was equivalent to the volume really involved by the moles of gas. Since the gas particles volumes rely upon the gaseous moles in the compartment, the expression that is deducted from the existent volume of the gas is equivalent to the number of moles of gas time’s b.

PV-nb= nRT

At the point when the gaseous pressure is small, and the gaseous volume is sensibly huge, the term nb on top condition is too little to even think about having any effect in the estimation. However, at elevated pressure, when the gaseous volume is little, the nb expression is rectified for the way that the volume of a non-ideal gas is bigger than the predictable ideal gas condition.

The assumption is there are no attraction forces connecting gas molecules can’t be valid. In the case of gases could never frame fluids. The gas particles are held together by the small intermolecular force amid the gas molecules. There are two outcomes for the intermolecular attraction,

• Gases consolidate to shape fluids at low down temperatures.
• The pressure of a non-ideal gas is negligible than anticipated amount of perfect gas.

Van der Waals introduced the pressure term in this condition because the pressure of a non-ideal gas is lesser than the probable ideal condition.

This condition furnishes a vastly improved behave of non-ideal gas than the perfect gas condition. The ideal gas condition is similarly legitimate for any gas, though the van der Waals condition contains a couple of constants a and b that change from one gas to another.

Deviations from perfect gas law can be portrayed by the van der Waals condition, which incorporates experimental constants to address the volume of the vaporous atoms and measure the decrease in pressure because of intermolecular forces. On the off chance that the temperature of a gas is diminished adequately, liquefaction happens, in which the gas gathers into a fluid-structure. Condensed gases have numerous business applications, remembering the vehicle of a lot of gases for little volumes and the employments of ultracold cryogenic fluids.

Context and Applications

This topic is important for postgraduate and undergraduate courses, particularly for Bachelors and Masters of Chemistry.

Practice Problems

 Question 1 : Find the false statement among the following.

(a) Charles’ law applies at constant temperature
(b) If the volume is increased at constant temperature the pressure of a given mass of gas decreases
(c) Isobaric changes are those which occur at constant pressure
(d) Boyle’s law applies at constant temperature

Answer: The false statement among the given statements is a.

Explanation: Charles's law expresses that at constant pressure, the gas volume is directly relative to the temperature.

Question 2: Find the false statement among the following.

1. An ideal gas is one that completely obeys the gas laws
2. Isothermal changes are those that occur at constant volume
3. The volume of a gas increases when the temperature increases at constant pressure
4. Changes that occur at constant pressure are called isobaric changes

Answer: The false statement among the given statements is 2.

Explanation: Isothermal changes are those that occur at a constant temperature.

Question 3: Under what conditions will a gas most closely follow ideal behavior?

1. Low pressure and high temperature
2. High pressure and low temperature
3. High pressure and high temperature
4. Low pressure and low temperature

Answer: The correct answer is low pressure and high temperature.

Explanation: Under high pressure and at low temperatures, ideal gas particles are forced closer together and intermolecular forces become a factor. When intermolecular forces also increase, since molecules move more slowly, similar to what would occur in a liquid state.

Question 4: Which of the following assumptions is not made by the ideal gas law?

1. The molecules move randomly
2. The molecules obey Newton's laws of motion at all times
3. The van der Waals forces are negligible
4. The intermolecular interactions follow the Coulomb model of electric repulsion

Answer: The correct answer is the intermolecular interactions follow the coulomb model of electric repulsion.

Explanation: The ideal gas law assumes only Newtonian mechanics, disregarding any intermolecular or electromagnetic forces.

Question 5: Which of the following factors does not explain why measurements of real gases deviate from ideal values?

1. Intermolecular forces
2. The volume between the gas particles
3. All of these factors will cause deviation from ideal values
4. The volume of the gas particles themselves

Answer: The volume between the gas particles.

Explanation: Measurements of real gases deviate from ideal gas predictions because intermolecular forces and the volume of the particles themselves are not taken into consideration for ideal gases.