How Do We Know When Force is Exerted?

The tension created on one body during push or pull is known as force.

Representation of Force

• In the direction of the effort due to the force applied.
• The force is represented with an arrow where the head of the arrow is in the direction of action.
• The magnitude of the force is denoted by the length of the vector ﴾arrow﴿.
• As it is known about effort, effort consists of one thing that is Equilibrium or Balance.
• By the property of vectors, we know that a vector quantity has both a magnitude and a direction.
• Now if the magnitude and the direction of the effort are same quantity then we call the effort balanced, then the resultant effort or net force on that body becomes zero. This is the equilibrium state.
• Now from this concept we also conclude that an object would remain in its state of rest or motion unless acted upon by an external force.

Condition of Equilibrium of Force on a Solid Body

• The LOA (line of action) must be on the same plane. i.e.-they must be coplanar.
• The line of action is convergent.

• In equilibrium state, the body is unaccelerated.

Initial Condition of Equilibrium

If in a body the resulting effort acting on it is zero, then we say that the body satisfies the equilibrium initial condition.

Let${\overrightarrow{F}}_1,{\overrightarrow{F}}_2\mathrm{.......}{\overrightarrow{F}}_n$effort acting on a body such that

Similarly, in terms of directions i.e. the x-direction and the y-direction, we get the components as –

For example,

• A pen is lying on a table.
• A clock hanging on a wall satisfies the first condition as it is at rest.

Secondary Equilibrium Condition

A body can still satisfy the equilibrium initial condition although the body is not at equilibrium. It is due to the tendency of the body to rotate.

Here a next condition arrives along with the first condition of the equilibrium. 

According to that condition ‘A body satisfies the secondary equilibrium condition when the net torque acting on the body becomes zero.

Numerically it is expressed as-

For example,

• The movement of the seesaw when children are sitting on it.
• The effort applied to the car steering.

If an object is moving with uniform velocity in a levelled road it is the example of equilibrium of forces.

Static Equilibrium

A body is considered to be in static equilibrium when the following conditions are satisfied

1. The total of the efforts on the object is zero.
2. The summation of the torques in all directions is zero.
3. Its linear momentum is zero.

Condition of Equilibrium of a System of Coplanar Parallel Forces:

• The algebraic sum of all the individual efforts must be equal to zero.
• About any point the algebraic sum of the moment of effort along the plane must be zero.ie- In clockwise and in the anticlockwise direction the sum of moment of the forces about a point is equal.

Formulas that can be used are-

There are three conditions that can satisfy the condition of non-concurrent effort-

1. At the horizontal direction the total of all effort is equal to zero. ${{\displaystyle \sum \overrightarrow{F}}}_x=0$

2. At the vertical direction the total of all effort is equal to zero.${\displaystyle \sum {\overrightarrow{F}}_y}=0$

3. The sum of the moment at any given point is zero. ${\displaystyle \sum {\overrightarrow{F}}_{\max }}=0$

Example: Let us consider two objects shown below. Here both the objects are in equilibrium but the individual efforts are not equal to each other.

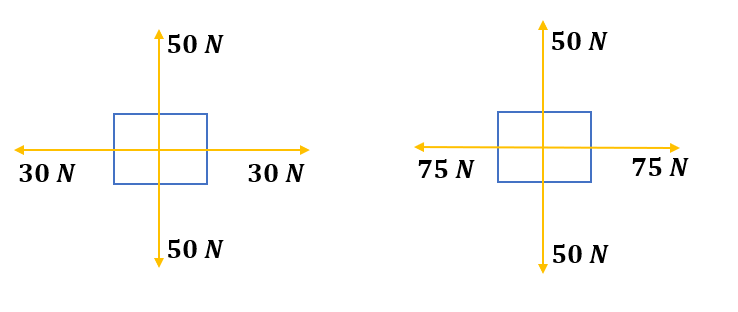
Common Mistakes

• Forces are vector quantities.
• Direction and magnitude are important.
• There are two conditions that must be met for an object to be in equilibrium forces.
• If the net effort is zero, the effort along any direction is zero.
• The magnitude of the torque about an axis is defined to be Τ=rFSinθ.

Formulas

Context and Applications

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for

• Bachelors in Technology (Mechanical Engineering)
• Masters in Technology (Mechanical Engineering)
• Bachelors in Technology (Civil Engineering)
• Masters in Technology (Civil Engineering)
• Bachelors in Science (Physics)
• Masters in Science (Physics)

Practice Problem

Problem 1: n forces are concurrent, each having a magnitude F, lying in the same plane and if two symmetrical efforts are removed, then what is the resultant of the (n-2) forces?

Solution: If n concurrent effort of equal magnitude acts on an object with equal angles between them, that each angle is equal to (360/n) degree, and in this case, the result becomes zero. Now if two consecutive efforts are removed then the resultant among them is: $\overrightarrow{F}$cos(cos(θ/2)).Hence when we remove the two consecutive efforts the symmetry gets disturbed. So finally, in this case the zero resultant now becomes - 2 $\overrightarrow{F}$cos(cos(θ/2)).

Problem 2: Let us consider a picture hanging on the wall; use the trigonometric function to determine the weight of the picture.

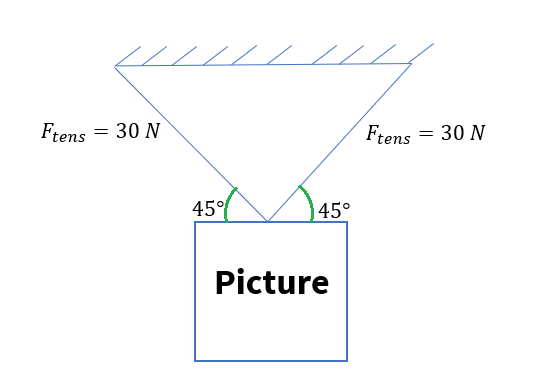
Solution:  It is given that, tension=40.0N and q= 45º.

Therefore,

• Hence each cable pulls upward with a force of 21.2N.
• Hence the picture weighs twice 21.2N that is -42.4N.

Problem 3: A signboard is hanging outside an auditorium, stating some directions. The signboard is hung using a horizontal bar and is supported properly. Consider the board to have a mass of 50 kg , determine the value of tension on the diagonal part of the cable.

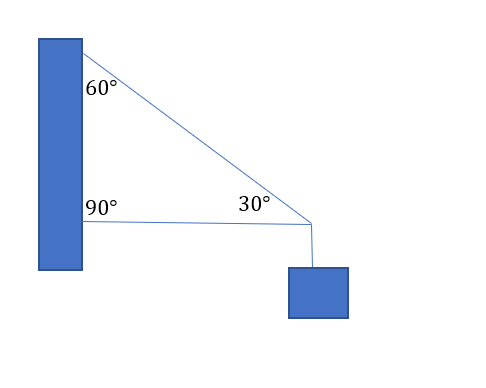
Solution- It is given that,

Mass=50kg.

Weight=490N.

As there is only “upward pulling” by the cable. It must behold all the upward effort. Thus the cable pulls it with 490N of effort.

Hence, 

This is the final result.

Problem 4: An inclined plane having angle of inclination as 30 degree which is smooth is placed on the surface of a truck. Consider the truck to move with an acceleration ‘’a’’. Suppose a block is placed on the inclined plane then find the acceleration of the block when it moves down the incline.

Solution- As when we analyze the motion with respect to a non-inertial frame of reference we use the pseudo force concept.

Therefore 

This gives the final result.

Problem 5: A person is pulling a cart of mass 100kg which is placed on a horizontal surface the surface is covered with snow where the coefficient of kinetic friction between the person pulling the cart and the snow is 0.1. Determine the tension in the string when the angle is 45 degrees and the cart moves with constant velocity.

Solution- Now according to the question

This gives the final result.